Test for Divisibility of Numbers
Test for Divisibility of Numbers: Overview
This topic covers concepts, such as, Divisibility by a Factor of a Divisor, Tests for Divisibility of Numbers, Divisibility of Sum and Difference of Two Numbers & Rule for Divisibility by Composite Numbers etc.
Important Questions on Test for Divisibility of Numbers
Prove the following property of divisibility:
If and are three natural numbers such that is divisible by , and is divisible by , then is divisible by also.
Explain the following property with the help of an example
If and are three natural numbers such that is divisible by , and is divisible by , then is divisible by also.
Explain the following property with the help of an example
If a number is divisible by another number, then it is divisible by each of the factors of that number.
Create two different four-digit numbers that are divisible by:
and
Let's write down the conditions of divisibility.
Conditions of divisibility by
The unit's digit of the number must be 
Sheela and her friends paid Rs. as fare to return home. If each pays equally, let's calculate how much each will have to pay.



 by
by
Then, let's divide by and see if it is divisible.
is  by
by
Each paid Rs. for the fare.
for the fare.
Studipo has bought kilogram of jalebis. He counted that there are jalebis. Let's see if of us can have equal members of jalebis without breaking any.


 by
by
Now let's see if is divisible by
Shikha bought one packet of toffees. She counted toffees in the packet. Let's see if of us can take equal members of toffees without having to break any.
 . divisible by
. divisible by
Would be divisible by then? Let's divide and find out.
So is divisible by .
Each of us got  toffees.
toffees.
Let's check divisibility by , without actually dividing.
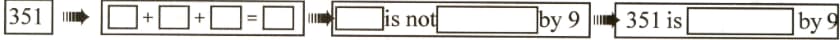
Let's check divisibility by , without actually dividing.

Let's check divisibility by , without actually dividing.
Let's check divisibility by , without actually dividing.

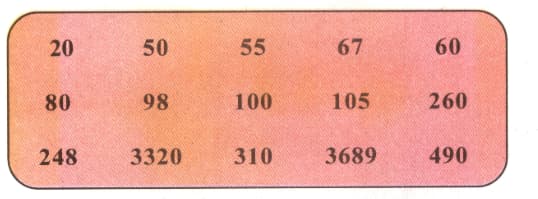
There are many numbers in the box below. Let's place them correctly in the boxes below,

Numbers divisible by

In the numbers below, lets () the numbers divisible by
We see that the number which have in the unit's place, when divided by , leave a remainder of 
The remainder is 
is  by
by
We see that the number which have in the unit's place, when divided by , leave a remainder of 
The remainder is 
is  by
by
We see that the number which have in the unit's place, when divided by , leave a remainder of 
The remainder is 
is  by
by
We see that the number which have in the unit's place, when divided by , leave a remainder of 
The remainder is 
is  by
by
We see that the number which have in the unit's place, when divided by , leave a remainder of 
The remainder is 
is  by
by
The number _____ is exactly divisible by .
